In this blog, I try to explain our paper PUPoW: A Framework for Designing Blockchains with Practically-Useful-Proof-of-Work & VanityCoin (arxiv version) in a simplified manner. Mathematical rigour and technical details are limited to what’s absolutely necessary to understand the basic idea and novelty in the paper.

Introduction

Bitcoin

Bitcoin is a decentralized ledger on a blockchain network. Many miners keep track of pending transactions, verify them and try to publish them in a block to get a reward in return. To decide who gets to mine a block, a proof-of-work (PoW) consensus protocol is used.

The idea behind PoW is to set the probability of a miner to mine a block equal to their fraction of the total computational power of the network so that spamming with multiple identities doesn’t give the spammer any unfair advantage. A block is required to be published every ten minutes due to security and latency reasons. In Bitcoin’s PoW, the miners are required to solve a partial hash pre-image problem, i.e., the hash of the block generated should be less than a target value.

Motivation for Proof-of-Useful-Work (PoUW) Protocols

As the price of Bitcoin increases, it becomes profitable to mine despite the competetion. Thus, a lot of electricity is used to find partial hash pre-images while mining every block. The amount of energy wasted just to achieve consensus seems inappropriate and makes one wonder if the partial hash pre-image problem can be replaced with some other useful problem. Such modified PoWs are known as proof-of-useful-work (PoUW) protocols. Note that there are other solutions (like proof of stake (PoS)) which don’t involve solving problems at all.

A lot of PoUW proposols (especially those involving ML) set problems which do not satisfy all the requirements of a PoW protocol. Those that do satisfy all the requirements don’t have a lot of applications as of now (like Prime Coin).

Practically Useful Proof of Work

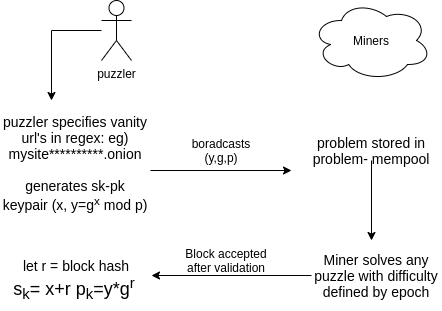
We define a problem as practically useful if someone is willing to pay for the problem to be solved. PUPoW is a framework where Bitcoin’s PoW has been modified to have another set of actors called as puzzlers who propose different instances of a problem type and miners solve the problem to receive a problem-solving fee from the puzzler in addition to the mining reward. Thus, the problem is not algorithmically generated unlike Bitcoin’s puzzle.

Let P be a problem type which a PUPoW blockchain uses for its PoW. Puzzlers can propose a problem p, an instance of P, (satisfying difficulty requirements) and broadcast it to the netword and add it in the problem mempool.

Adapting a problem type to be used for PoW

We require the problem to be a partial inverse problem, i.e., given a set of acceptable outputs, we need to need to find any corresponding input. We then find a way to interpret hash of block as an input value. For example, if we want inputs to a univariate function f() to be less than some target t,

do{
    h = Hash(block_header); // let h be a 32 bit integer
} while (f(h) <= t);

Here we interpret the hash as a 32 bit integer and the domain of f() is also 32 bit integers. We discuss other examples in the paper. Finding vanity addresses is another example of such a problem type.

VanityCoin

Vanity Addresses

TOR URLs and Bitcoin wallet addresses are generated by sampling a random private key which gives a corresponding public key (url/address). Unlike indexed web, a url generated from a private key can’t be chosen to have any pattern. The only way to have a public key of choice is to sample a lot of private keys and pick the most suitable address.

Adapting TOR Vanity URL for PUPoW

A naive way would be to use the above method as it is, where h is treated as the private key and the public key, f(h) should follow the pattern described by the puzzler.

Note that $f(h) = g^h$, where g is the generator. This is a simplification but will be enough to understand the intuition behind VanityCoin. A prerequisite to understand the next paragraph: discrete log problem.

This will result in the private key h being available to everyone in the network. To keep the private key a secret, the puzzler samples some random x and puts $y_0 = g^x$ in the problem description. Miners sample h and find a y satisfying the pattern, where $y = f’(h) = y_0 * g^h = g^{(x+h)}$. Due to this, the puzzler gets a suitable url and the corresponding private key X = (x+h) remains a secret as only the puzzler knows the value of x.

This is the first draft of the summary. Let me know if anything can be improved. All technical details can be found in the paper (arxiv version).